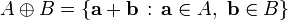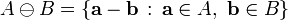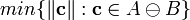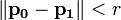Darwinbots3/Physics/Detection

Consider the case where all objects in the world are static (not moving). Suppose we want to find a list of bodies which might be colliding. This list might have false positives, but it's much cheaper than the complete collision test. Finding this list of maybe collisions is called broad phase collision detection. The complete collision test where the possibility of false positives and false negatives is eliminated is called narrow phase collision detection.

Broad phase collision detection

This is a mostly comprehensive list of methods for broad phase collision detection:

Naive

The naive broad phase algorithm is just to assume that all bodies might be colliding with each other. The first body is tested against the second, third, fourth, ... nth. The second body is tested against the third, fourth, ... nth. For a total of 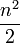$\frac{n^2}{2}$ narrow phase collision checks.

The primary advantage to this method is its simplicity to implement and no memory overhead. The downside is that the operation is 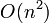$O(n^2)$, which makes anything more than about 1000 bodies too slow.

Uniform grid

A uniform grid (also sometimes called a spatial hash) divides the universe into a regular grid of boxes, like a chess board. Each grid square has a list of bodies which are at least partially inside that grid square.

If there are more bodies than grid squares:

For each grid square
  For each pair of bodies in that grid square
    Pass that pair on to narrow phase collision detection

(Watch out for colliding the same pair more than once).

If there are more grid squares than bodies:

 For each body
   For each grid square that body overlaps
     For each otherBody in the current gridSquare
       Pass this body and otherBody on to narrow phase

(Again watch out for colliding the same pair more than once. If each body has a unique serial number, you can just test that the serial number for this body is < the serial number for otherBody).

Worst case performance is still 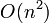$O(n^2)$ in the case where all bodies are in the same grid square. Average case performance is 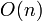$O(n)$. It's important to choose an appropriate size for the grid squares. Too large and it's too permissive about passing collisions on to narrow phase. Too small and it starts to waste lots of memory. It also works best when the bodies are all approximately the same size.

Sources: 1 2

Hierarchical grid

An extension of uniform grids from above. A grid size is chosen to be as small as possible without burning too much memory. Above this is constructed a larger grid such that four of the smaller grid squares fit in one of these larger grid squares. This continues recursively up to the very top level. Bodies are placed on the smallest grid level such that they take up only 4 or fewer grid squares.

The primary advantage over uniform grids is a better handling of large bodies. Worst case performance is still 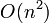$O(n^2)$, though it becomes harder to reach worst case. Average case is still $O(n)$.

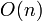Sort and sweep

By using the separating axis theorem, we know that a necessary (but not sufficient) condition for two bodies colliding is that their projections onto an arbitrary axis also collide. If we project all bodies on to arbitrary axes, and then sort the results in a linked list, it becomes an 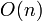$O(n)$ operation to find possible collision pairs. Adding axes allows the test to become more accurate.

The algorithm looks like:

For each body
  Find projection of body on to axis.  Projection is in form of interval (min and max bounds)
  Add min bounds to linked list
  Add max bounds to linked list

Sort the list(s)

For each list
  For each entry in list
    if entry is a min bounds
      body = body which created entry
      otherEntry = entry->next
      while(otherEntry != max bounds for body)
        add body and otherEntry's body to this list's collection of possible collisions
        otherEntry = entry->next

pass to narrow phase any collision pairs which appear in all lists' collections of possible collisions

The primary advantage over grid methods is memory use. The linked lists scale linearly with the number of bodies. Likewise finite bounds for the universe aren't necessary, so it becomes a reasonable method for things like a simulation of stars.

If the axis are chosen poorly it can degenerate in to 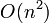$O(n^2)$, though the more axis chosen the less the chance for this. Too many axis can also be a problem too, since searching all the possible collision lists is an 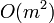$O(m^2)$ operation for 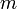$m$ lists. Though this can be made into a 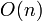$O(n)$ order operation by using a hash table to find hash conflicts between the possible collision lists.

Naively sorting the lists every cycle is a 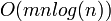$O(m n log(n))$ operation. However by saving the lists between cycles and realizing that most bodies will not have changed order too much (temporal and spatial coherence), the sort comes down to a 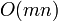$O(m n)$ operation.

So similar to grid methods the average case should be 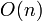$O(n)$, though in practice grid methods should do a better job of culling collisions.

It is usually a good idea to choose axis that are not the x or y axis, since bodies will tend to clump along the y axis (think lots of balls sitting at the bottom of the screen) and x axis (think a vertical stack of bodies). If two axis are used, they should be orthogonal to each other. More than two I'm not sure, but probably evenly distributed on the unit circle is a good idea.

Hash sort

Sort of a combination of the grid methods and sort and sweep. Just like with the sort and sweep, bodies are projected against arbitrary axes. However instead of adding the results to a linked list, each axis has a hash table. Possible collisions are found by examining hash collisions.

The primary advantage over a linked list is that the sorting is done implicitly, which eliminates a large amount of computation. The primary disadvantage over a linked list is that the universe must be finitely bounded like with grid methods. Though it requires considerably less memory.

Just like with a grids, a hierarchical hash table can be used instead of a uniform hash table. The smallest level in the hash table such that the body takes up at most two cells is chosen.

Implicit grid

In the grid methods outlined before, each grid square has its own linked list of bodies inside it. This works well in practice, but requires the universe to be bounded, and can potentially require a large amount of wasted memory from empty grid squares.

An alternative technique is to create a hash function which maps a grid square into a one dimensional array (hash table) of linked lists. As long as a good hash function is used, the effect is roughly the same as normal grid methods, with the downside that computing which hash cell to look at requires a bit more computation.

It then becomes an easy matter to extend our hash function to the range of all possible grid squares in an unbounded universe. The simplest method simply being to mod the grid square indicies by some given value. This allows us to use a grid method even in an unbounded universe.

Since two grid squares can map to the same hash cell, it becomes even more important to test bounding volumes against each other to early out of collision tests, since two objects in the same list might be quite far away from each other.

The number of cells chosen is something of an art.

Narrow phase collision

Minkowski sum

The Minkowski sum is a way to combine the shapes of two objects into a single larger object. This is often useful because it allows us to change from a test of collision between two complicated shapes to a test of collision between a point and a single slightly more complicated shape.

The Mikowski sum is defined as:

$A \oplus B = \{\mathbf{a}+\mathbf{b}\, : \,\mathbf{a}\in A,\ \mathbf{b}\in B\}$

Minkowski difference

The Minkowski difference is defined likewise:

$A \ominus B = \{\mathbf{a}-\mathbf{b}\, : \,\mathbf{a}\in A,\ \mathbf{b}\in B\}$

It is useful because two objects are in collision iff the origin is contained in the convex shape formed by their Minkowski difference. And even more importantly, computing the minimum distance between two objects is equivalent to computing the minimum distance between the Minkowski difference and the origin.

That is, the distance between A and B is:

$min \{ \| \mathbf{c} \| : \mathbf{c} \in A \ominus B \}$

Point to circle

Given a point 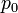$p_0$ and a circle with center 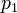$p_1$ and radius $r$, the point is inside the circle iff:

$\| \mathbf{p_0} - \mathbf{p_1} \| < r$

Circle to Circle

This collision test is quite easy. We take the Minkwoski sum of the two circles to form a single larger circle of radius 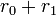$r_0 + r_1$. We've converted our circle to circle collision test to a point to circle collision test.