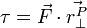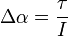Darwinbots3/Physics
Basic concepts
Forces' linear affects
Any force acting on a body, at any point on a body, applies the same change in acceleration to the body's center of mass. Consider the diagram below:
__________ | | | | | X | <---| | |________| <---
Diagram 1
Where X is the center of mass for the body. 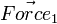 is exactly centered, so it produces no torque. The change in acceleration of the body's center of mass is given by
is exactly centered, so it produces no torque. The change in acceleration of the body's center of mass is given by 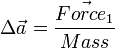 .
.
Let 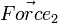 have the same magnitude and direction as
have the same magnitude and direction as 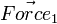 . However it's applying its force at a different point on the body, and will produce torque. Even though it's off center, the change in acceleration for the body's center of mass is still
. However it's applying its force at a different point on the body, and will produce torque. Even though it's off center, the change in acceleration for the body's center of mass is still 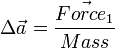 .
.
Forces' angular affects
Consider Diagram 1 again. 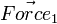 will not produce any change in angular acceleration for the body, because it is centered.
will not produce any change in angular acceleration for the body, because it is centered. 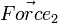 will produce change in angular acceleration, because it is off center. In general, the torque (
will produce change in angular acceleration, because it is off center. In general, the torque (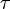 ) produced by a force is given by:
) produced by a force is given by:
And the change in angular acceleration is given by:
Where:
-
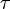 is the scalar torque term.
is the scalar torque term. -
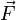 is the vector Force term.
is the vector Force term. -
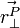 is the vector perpendicular to the vector from the body's origin to the place
is the vector perpendicular to the vector from the body's origin to the place 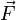 is acting on the body.
is acting on the body. -
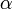 is the scalar angular acceleration
is the scalar angular acceleration -
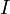 is the body's scalar moment of inertertia.
is the body's scalar moment of inertertia.
Collision
Consider a collision between two bodies: body A and body B. It is possible to show that the impulse from the collision is given by the solution to:
- <math>