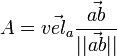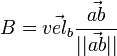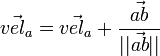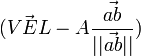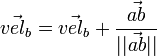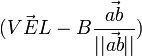New tie paradigm
For the C++ version (2.5), all old tie sysvars are thrown out. Here's the comprehensive list of all the new tie commands and sysvars:
Contents
Basics
Soft ties, such as birth ties and ties under 100 cycles old, act as springy telescoping rods. They will constantly push to return to their creation length, though this force is damped to achieve stability.
Hard ties are totally rigid bodies, with a set length. Bots can "flash" the tie for a cycle, allowing it to change length. Bots apply a force along the length of the tie. After this, the tie ceases to exist for a cycle, allowing the bots on either end to move to a new position. The tie then reappears, and carries on as normal.
Ties connect to bots using a radial bearing, so that the rotation of the tie and the rotation of the bot are independent of each other. Bots can "freeze" the the bearings of hard ties, basically locking the tie and the bot together. This can be done to "freeze" the relative angles of a tie with respect to the bot.
Bots can apply forces to two hard ties to change the angle between them, rather similar to how muscles are used to move bones in the human body (the specifics of this are still in progress).
Commands
- readtie - If settie is set (ie: not 0) writetie takes 1 value from the stack, representing the memory location to be read from, and places a value on the stack representing the value at that location through the tie. If settie is positive, and points to a phase representing more than one tie, the returned values are averaged for each robot thus pointed to.
- .nrg readtie will read the value stored in .nrg from the bot connected through the current tie.
- writetie - If settie is set (ie: not 0) writetie takes 2 values from the stack. 10 .up writetie will place 10 at the location specified (.up) in whichever bots are at the other end of the tie(s) settie addresses.
- When settie isn't set, writetie removes an extra value from the stack to represent the tie being pointed to. ie: -1 10 .up writetie to write to tie -1.
- If a negative memory location is specified (ie: 10 -1 writetie) substance transfer is initiated. 10 -1 writetie would transfer 10 units of energy from the tie being pointed to. If settie is unset, this version also takes an additional value form the stack.
- settie - Sets the current tie that the DNA is looking at. When a new tie is set, all the sysvars update for the new information from that tie. Negative numbers specify a physical tie in the internal array. Positive numbers specifies a tie phase. Multiple ties can be addressed through a single tie phase.
- nexttie - settie's to the next tie. If settie is currently set to negative (ie: internal arrays) it finds the next tie in the internal array. If the present tie is already at the end, it moves back to the beginning. If the present tie is positive, nexttie finds the next valid tie phase, looping back to the lowest tie phase if it's already at the highest. If settie is unset (ie: set to 0) nexttie pushes it to first internal tie (ie: a negative).
Sysvars
- tielen - A read/write sysvar. reads back the ties natural length. If this value is overwritten, the ties natural length is set to the new value.
- tieangle - A read sysvar. Reads back the relative angle of the tie with respect to the bot's eye.
- tie - Attempts to form a tie with the specified phase. Since phases are limited to [1, 200], a value greater than 200 will be modded by 200. A negative value's sign will be flipped then modded 200.
- deltie - If settie is set and the number stored is non negative, the current tie(s) selected are deleted. If settie is not set, the tie phase (positive values) or tie index (negative values) matching the value is deleted.
- currtie - The value that settie is set to. A read sysvar.
- numties - Returns the number of physical ties connected to the bot.
- recentport, recentphase - Returns the phase and port of the most recently formed tie with a cycle delay.
Sharing
MB sharing as it was in 2.4 and before does not exist. MB sharing uses the same mechanism that tie feeding uses, though ties that have hardened have a drastically increased bandwidth.
Tie Notes
- Ports - The internal array index is referred to as a tie's "port". Each tie has a unique port. Each port may or may not have a tie. Port ranges are set by the number of ties in existence when a new tie is formed. Ties always fill in the first gap in the internal tie array.
- Phase - The phase of a tie is a way of addressing multiple ties at once. Each tie has a unique phase. Phases may exist anywhere in the mod range [1,200]. That is, 1 = 201 = 401.
- Length - Ties cannot be longer than 1000 twips (a typical bot is 120 twips in diameter). This includes birth ties. Later the max tie length will be a function of the amount of material (nrg) used in its construction. Ties' diameter will stretch and shrink as the tie does. Ties won't be allowed to go below a certain diameter. This diameter will also effect the bandwidth (that is, the max throughput) allowed in sharing/stealing substances.
- Birth Ties - Spring ties that after 100 cycles die off or harden depending on the value set on birthtietype. Birth ties are only formed between a mother and child bot at the moment of reproduction.
Tie Physics
Tie physics has been a lot of work, and a lot of calculus, but I think the below is accurate. It still will need to be double checked, as it's been many months since I did the work.
Fluid forces on ties can be segmented into two separate parts: those that cause rotation of the tie and those that cause translation of the tie.
Ties are defined by two endpoints, the two bots.
Quantities
- (note, for ease of expression sign(a) has been expressed as
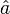 for scalars)
for scalars) 
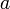 = velocity of bot A with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(A).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
= velocity of bot A with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(A).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
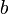 = velocity of bot B with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(B).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
= velocity of bot B with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(B).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
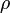 = density of fluid given in mass per cubic twip Failed to parse (unknown function "\LARGE"): \LARGE \frac{Mass}{twip^3}
= density of fluid given in mass per cubic twip Failed to parse (unknown function "\LARGE"): \LARGE \frac{Mass}{twip^3}
 = radius of tie
= radius of tie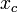 = center of gravity for tie. = Failed to parse (unknown function "\LARGE"): \LARGE \frac{L * mass2} {mass1 + mass2}
= center of gravity for tie. = Failed to parse (unknown function "\LARGE"): \LARGE \frac{L * mass2} {mass1 + mass2}
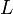 = length of tie
= length of tie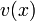 = velocity of tie at
= velocity of tie at  distance away from bot a
distance away from bot a
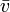 = the average absolute value of velocity of the tie as a whole.
= the average absolute value of velocity of the tie as a whole.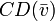 = Drag coefficient for the tie using average velocity
= Drag coefficient for the tie using average velocity- Failed to parse (unknown function "\LARGE"): \LARGE \bar{v} = \frac{\int_0^L{|v(x)|}}{L}
Maple gives:
int( abs(v(x)) / L, x = 0..L); =
2 2
(-b signum(b) + a signum(a))
1/2 --------------------------------
-b + a
or Failed to parse (unknown function "\LARGE"): \LARGE \frac{a^2 \hat{a} -b^2 \hat{b}}{2(a-b)}
Translational Drag
Translational drag slows a tie moving through the liquid. For instance, if two bots are moving with identical velocity vectors that are not parallel to the tie between them, translational drag on the tie would serve to slow these two bots down.
Failed to parse (unknown function "\Large"): \Large Force_{Drag} = \rho r CD(\bar{v}) \int_0^L{v(x)^2 \hat{v(x)} dx}
if a != b then Integral = Failed to parse (unknown function "\LARGE"): \LARGE \frac {L(a^3 \hat{a} - b^3 \hat{b})} {3(a-b)}
if a = b then Integral =
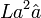
Translational force is divided up between bot A and B depending on their masses and distance from xc.
Integrals are found using Maple 5.1 and simplifying. Maple gives Integral =
int( v(x) * abs(v(x)), x = 0..L) =
3 3
L (-b signum(b) + a signum(a))
1/3 --------------------------------
-b + a
If a = b, the limit is given as
a^2*signum(a)*L
Rotational Drag
Rotational Drag only effects the rotational inertia of the tie, not it's translational motion. Basically it slows a spinning tie down.
This is much more of a head scratcher, but this is what I came up with:
Failed to parse (unknown function "\LARGE"): Force_{Drag} = \LARGE \rho r CD(\bar{v}) \int_0^L{v(x)^2 \hat{v(x)} (x - x_c) dx}
Maple 5.1 gives the above Integral as:
int( v(x) * abs(v(x)) * (x - xc), x = 0..L) =
4 3 4
1/12 L (3 b signum(b) L - 4 b signum(b) a L - 4 b signum(b) xc
3 4 4
+ 4 b signum(b) xc a - 4 a signum(a) xc + a signum(a) L
3 / 2
+ 4 a signum(a) xc b) / (-b + a)
this is the above (hopefully, there might be a typo) in more readable math: Failed to parse (unknown function "\HUGE"): \HUGE \frac{L}{12} \frac{3 b^4 \hat b L - 4 b^3 \hat b a L - 4 b^4 \hat b x_c + 4 b^3 \hat b x_c a - 4 a^4 \hat a x_c + a^4 \hat a L + 4 a^3 \hat a x_c b}{(a-b)^2}
and factoring out 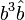 and
and 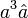 :
:
Failed to parse (unknown function "\HUGE"): \HUGE \frac{L}{12} \frac{ b^3 \hat b (3bL - 4aL - 4bx_c + 4ax_c) + a^3 \hat a (4ax_c + aL + 4bx_c)}{(a-b)^2}
Rotational Drag is also divided up between bot A and B depending on their masses and distance from xc.
Note that if a = b, Rotational Drag is 0 (since the tie isn't rotating).
Rigid Tie velocity normalization
Rigid ties means that bots' velocities will be normalized across the tie in addition to their positions being kept within a certain constraint.
Here's how the velocity normalization works:
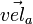 = velocity of bot a
= velocity of bot a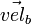 = velocity of bot b
= velocity of bot b
- Find velocity parallel to ab.
-
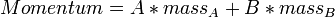
- Failed to parse (unknown function "\LARGE"): \vec{VEL} = \LARGE \frac{Momentum} {mass_A + mass_B}
-
Conclusion
The exact way in which the drags are divided up I haven't worked out yet, but I don't imagine it should be too terribly difficult (jinxed myself :P).
The main theoretical issue I have is with the possibility that I'm doubling up the forces by calculating both the translational and rotational Drag separately and applying them separately, but I don't think this is the case, and even if it is it's just increasing by a constant factor, which is a minor issue.
Tie physics (redone)
Notations and definitions
A tie between botA and botB is uniquely specified by the position and velocity of its endpoints, the bots' centers. Let's call:
- rA and rB the position of botA and botB (botA.pos and botB.pos in the code)
- vA and vB their velocities (botA.vel and botB.vel in the code)
- L = ||rB-rA|| the length of the tie and u the unit vector such that rB-rA = L u.
- n the ?/2-rotation of u, so that (u, n) is a direct orthonormal base. We'll denote the components of any vector x in this base as x = xT u + xNn
Let's also label the points of the ties by a parameter x in [0;1]. r(x) = rA +L x u and the corresponding velocity is v(x) = (1-x)vA + x vB.
Now, the drag force acting on an infinitesimal portion of the tie between the positions r(x) and r(x+dx) is dF = -L dx . f |v.n|α - 1 (v.n) n, with α = 1 if viscosity is the dominating influence on drag and α = 2 if it's turbulence. f is a coefficient defining the magnitude of drag, it is assumed independent of the length of the tie.
Assuming that the tie is massless, we can then solve the equations of motions for the tie to get the forces applied on the bots: both the sum of the forces and the sum of the torques applied to it are zero.
Drag forces
Let's call FA and FB the forces applied by the tie on the bots. The tie is subjected to forces -FA, -FB and Failed to parse (syntax error): {\bf F}=\int {\bf dF} . We have F = FA + FB.
Failed to parse (syntax error): {\bf F} = -\int_0^1 L f |w_A + x (w_B - w_A)|^{\alpha - 1} (w_A + x (w_B - w_A)) dx {\bf n}
Failed to parse (syntax error): {\bf F} = -\frac{L f}{(\alpha + 1)(w_B - w_A)} (|w_B|^{\alpha - 1} w_B^2 - |w_A|^{\alpha - 1} w_A^2 ) {\bf n}
Let's compute the torques about A: Failed to parse (syntax error): {\bf T} = \vec{AB} \wedge {\bf F}_B with Failed to parse (syntax error): {\bf T} = \int \vec{AM} \wedge {\bf dF}
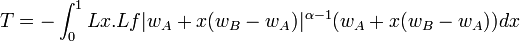 We get:
We get:
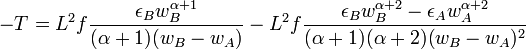 with ε = sign(wα+1).
with ε = sign(wα+1).
If α = 1, all the signs are positive and we have:
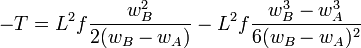
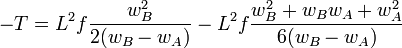
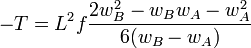
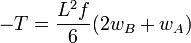
Thus, finally, 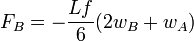 and
and 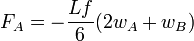 .
.
If α = 2, it gets more complicated and we must distinguish between two cases:
If wA and wB have the same sign,
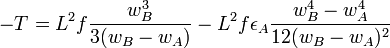
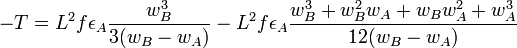
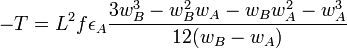
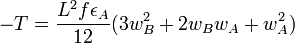 and
and 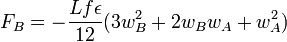
If wA and wB have opposite signs,
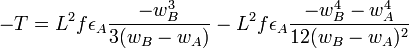
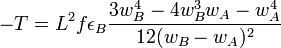 and
and 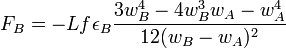 , with no possible simplification.
, with no possible simplification.