Difference between revisions of "New tie paradigm"

Revision as of 19:36, 4 May 2006

For the C++ version (2.5), all old tie sysvars are thrown out. Here's the comprehensive list of all the new tie commands and sysvars:

Basics

Ties are considered to be perfectly rigid telescoping rods. They connect to bots using a radial bearing, so that the rotation of the tie and the rotation of the bot are independant of each other. Bots can "freeze" the the bearing with specific ties, basically locking the tie and the bot together. This can be done to "freeze" the relative angles of two ties.

Bots can apply forces to two ties to change the angle between them, rather similar to how muscles are used to move bones in the human body.

Commands

• readtie - If settie is set (ie: not 0) writetie takes 1 value from the stack, representing the memory location to be read from, and places a value on the stack representing the value at that location through the tie. If settie is positive, and points to a phase representing more than one tie, the returned values are averaged for each robot thus pointed to.

.nrg readtie will read the value stored in .nrg from the bot connected through the current tie.

• writetie - If settie is set (ie: not 0) writetie takes 2 values from the stack. 10 .up writetie will place 10 at the location specified (.up) in whichever bots are at the other end of the tie(s) settie addresses.

When settie isn't set, writetie removes an extra value from the stack to represent the tie being pointed to. ie: -1 10 .up writetie to write to tie -1.

If a negative memory location is specified (ie: 10 -1 writetie) substance transfer is initiated. 10 -1 writetie would transfer 10 units of energy from the tie being pointed to. If settie is unset, this vesion also takes an additional value form the stack.

• settie - Sets the current tie that the DNA is looking at. When a new tie is set, all the sysvars update for the new information from that tie. Negative nubmers specify a physical tie in the internal array. Positive numbers specifies a tie phase. Multiple ties can be addressed through a single tie phase.
• nexttie - settie's to the next tie. If settie is currently set to negative (ie: internal arrays) it finds the next tie in the internal array. If the present tie is already at the end, it moves back to the beginning. If the present tie is positive, nexttie finds the next valid tie phase, looping back to the lowest tie phase if it's already at the highest. If settie is unset (ie: set to 0) nexttie pushes it to first internal tie (ie: a negative).

Sysvars

• readtielen - A read sysvar. Reads back the length of the current tie.

• writetielen - A read/write sysvar. reads back the ties natural length. If this value is overwritten, the ties natural length is set to the new value.

• tieangle - A read sysvar. Reads back the relative angle of the tie with respect to the bot's eye.

• tie - Attempts to form a tie with the specified phase. Since phases are limited to [1, 200], a value greater than 200 will be modded by 200. A negative value's sign will be flipped then modded 200.

• deltie - If settie is set and the number stored is non negative, the current tie(s) selected are deleted. If settie is not set, the tie phase (positive values) or tie index (negative values) matching the value is deleted.

• currtie - The value that settie is set to. A read sysvar.

• numties - Returns the number of phsyical ties connected to the bot.

• recentport, recentphase - Returns the phase and port of the most recently formed tie with a cycle delay.

Sharing

MB sharing as it was in 2.4 and before does not exist. MB sharing uses the same mechanism that tie feeding uses, though ties that have hardened have a drastically increased bandwidth.

Tie Notes

• Ports - The internal array index is referred to as a tie's "port". Each tie has a unique port. Each port may or may not have a tie. Port ranges are set by the number of ties in existance when a new tie is formed. Ties always fill in the first gap in the internal tie array.

• Phase - The phase of a tie is a way of addressing multiple ties at once. Each tie has a unique phase. Phases may exist anywhere in the mod range [1,200]. That is, 1 = 201 = 401.

• Length - Max tie length will be 1000, after which all ties become 100% rigid and acts like a stiff rod. This includes birth ties. A later feature will be that the max tie length is a function of the amount of material (nrg) used in its construction. Ties' diameter will stretch and shrink as the tie does. Ties won't be allowed to go below a certain diameter. This diameter will also effect the bandwidth (that is, the max throughput) allowed in sharing/stealing substances.

• Birth Ties - Spring ties that after 100 cycles die off or harden depending on the value set on birthtietype. Birth ties are only formed between a mother and child bot at the moment of reproduction.

Tie Physics

Tie physics has been alot of work, and alot of calculus, but I think the below is accurate. It still will need to be double checked, as it's been many months since I did the work.

Fluid forces on ties can be segmented into two seperate parts: those that cause rotation of the tie and those that cause translation of the tie.

Ties are defined by two endpoints, the two bots.

Quantities

• (note, for ease of expression sign(a) has been expressed as 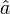for scalars)
• 
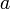• = velocity of bot A with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(A).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
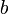• = velocity of bot B with respect to the tie, a scalar quantity = Failed to parse (unknown function "\LARGE"): bot(B).\vec{vel} \times \LARGE \frac{ \vec{ab}}{||ab||}
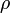• = density of fluid given in mass per cubic twip Failed to parse (unknown function "\LARGE"): \LARGE \frac{Mass}{twip^3}
• = radius of tie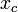
• = center of gravity for tie. = Failed to parse (unknown function "\LARGE"): \LARGE \frac{L * mass2} {mass1 + mass2}
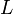• = length of tie
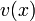• = velocity of tie at 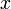distance away from bot a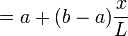
• = the average absolute value of velocity of the tie as a whole.
• = Drag coefficient for the tie using average velocity
• Failed to parse (unknown function "\LARGE"): \LARGE \bar{v} = \frac{\int_0^L{|v(x)|}}{L}

Maple gives:

int( abs(v(x)) / L, x = 0..L); = 
                       2              2
                    (-b  signum(b) + a  signum(a))
                1/2 --------------------------------
                                 -b + a

or Failed to parse (unknown function "\LARGE"): \LARGE \frac{a^2 \hat{a} -b^2 \hat{b}}{2(a-b)}

Translational Drag

Failed to parse (unknown function "\Large"): \Large Force_{Drag} = \rho r CD(\bar{v}) \int_0^L{v(x)^2 \hat{v(x)} dx}

if a != b then Integral = Failed to parse (unknown function "\LARGE"): \LARGE \frac {L(a^3 \hat{a} - b^3 \hat{b})} {3(a-b)}

if a = b then Integral =

Translational force is divided up between bot A and B depending on their masses and distance from xc.

Integrals are found using Maple 5.1 and simplifying. Maple gives Integral =

int( v(x) * abs(v(x)), x = 0..L) = 
                         3              3
                    L (-b  signum(b) + a  signum(a))
                1/3 --------------------------------
                                 -b + a

If a = b, the limit is given as

a^2*signum(a)*L

Rotational Drag

This is much more of a head scratcher, but this is what I came up with:

Force Drag = p * r * CD(V) * Integral(v(x)^2 sgn(v(x)) (x - xc) dx) from 0 to L

Maple 5.1 gives the above Integral as:

int( v(x) * abs(v(x)) * (x - xc), x = 0..L) = 
            4                  3                    4
 1/12 L (3 b  signum(b) L - 4 b  signum(b) a L - 4 b  signum(b) xc
             3                     4                 4
        + 4 b  signum(b) xc a - 4 a  signum(a) xc + a  signum(a) L
             3                   /         2
        + 4 a  signum(a) xc b)  /  (-b + a)
                               /

where xc = (mass2 * L) / (mass1 + mass2)

Rotational Drag is also divided up between bot A and B depending on their masses and distance from xc.

Rigid Tie velocity normalization

Rigid ties means that bots' velocities will be normalized across the tie in addition to their positions being kept within a certain constraint.

Here's how the velocity normalization works:

• ab = posB - posA
• vela = velocity of bot a
• velb = velocity of bot b

1. Find vel vectors parallel to ab.
   1. ab / ||ab|| * a = A
   2. ab / ||ab|| * b = B
   3. A,B are scalars (from dot product)
2. Momentum = A * massA + B * massB
3. VEL = Momentum / (massA + massB)
4. 1. vela += ab / ||ab|| * (VEL - ab / ||ab|| * A)
   2. velb += ab / ||ab|| * (VEL - ab / ||ab|| * B)

Conclusion

The exact way in which the drags are divided up I haven't worked out yet, but I don't imagine it should be too terribly difficult (jinxed myself :P).

The main theoretical issue I have is with the possibility that I'm doubling up the forces by calculating both the translational and rotational Drag seperately and applying them seperately, but I don't think this is the case, and even if it is it's just increasing by a constant factor, which is a minor issue.

Tie physics (redone)

Notations and definitions

A tie between botA and botB is uniquely specified by the position and velocity of its endpoints, the bots' centers. Let's call:

• r_A and r_B the position of botA and botB (botA.pos and botB.pos in the code)
• v_A and v_B their velocities (botA.vel and botB.vel in the code)
• L = ||r_B-r_A|| the length of the tie and u the unit vector such that r_B-r_A = L u.
• n the ?/2-rotation of u, so that (u, n) is a direct orthonormal base.

Let's also label the points of the ties by a parameter x in [0;1]. r(x) = r_A +L x u and the corresponding velocity is v(x) = (1-x)v_A + x v_B.

Now, the drag force acting on an infinitesimal portion of the tie between the positions r(x) and r(x+dx) is dF = f |v.n|^{α - 1} (v.n) n, with α = 1 if viscosity is the dominating influence on drag and α = 2 if it's turbulence. f is a coefficient defining the magnitude of drag, it is assumed independent of the length of the tie.